| Main authors: | Bautista, S., Urghege, A.M., Camacho, A., Turrión, D., Jaime, L., Vera, M.A., Nazarova, V., Vega-Rosete, S., Sáez-Cases, A., Fuster, A., Morcillo, L., López-Poma, R., Valera, M., D. Fuentes, and Rodríguez, F., Bladé, C. and Mayor, A.G. |
| Editor: | Jane Brandt |
| Source document: | Bautista, S. et al. (2017) Dryland restoration dynamics and thresholds as a function of plant pattern and diversity. CASCADE Project Deliverable 4.3 31 pp |
To analyze the main basic effects of global and local feedbacks on the recovery potential of degraded drylands, we used the mean field approximation (Morozov and Poggiale, 2012) to an extension of a well-known spatially explicit dryland model that exhibits catastrophic transitions (Kefi et al. 2007b; hereafter BCA model), with the incorporation of global and local feedbacks. The BCA model is a stochastic cellular automaton that represents a dryland ecosystem by a grid of vegetated, empty or degraded cells. Empty cells represent bare soil that is suitable for plant colonization, while degraded cells represent eroded soil that cannot be colonized by vegetation. The model represents local facilitation (i.e., the positive effect of vegetation on its local environment) as an increased regeneration rate of degraded cells when they are close to vegetated cells. The colonization rate of empty cells depends on a parameter (b) that reflects the external pressure on the system.
The incorporation of global feedbacks into the BCA model was carried out in Mayor et al. (2013) in the framework of CASCADE, through the use of the hydrological connectivity index Flowlength (Mayor et al. 2008) as a proxy for the net loss of resources from the system, affecting the behaviour of the vegetated patches as:
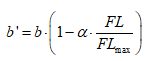
where b' is the plant establishment as affected by the net loss of resources from the system; b is the potential plant establishment, which coincides with plant establishment in the original model of Kéfi et al. (2007b); α represents the strength of the feedback between plant functioning and vegetation pattern via the global loss of resources; FL is the global connectivity (measured as the Flowlength index); and FLmax is the maximum value of the global connectivity. The resulting model (hereafter GCA model) was also a cellular automata model, allowing investigating the effect of the global feedback by simulations for specific sets of parameters.
The incorporation of local feedbacks was carried out in the model ECOHYDRY (Mayor et al., in preparation), considering the redistribution of resources mediated by the hydrological connectivity, and using the Flowlength arriving to each cell of the grid as a proxy of the transfer of resources from bare to vegetated patches, affecting the behaviour of the vegetated patches as:
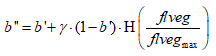
where b’’ is plant establishment as affected by both local and global feedbacks; γ represents the strength of the feedback between plant functioning and vegetation pattern via the local gain of resources; flveg is the local connectivity of neighbouring vegetated cells; flvegmax is the maximum value of the local connectivity of neighbouring vegetated cells; and H is a saturation function accounting for a nonlinear behavior of the local gains, attaining maximum effects from above a certain connectivity level.
To be able to derive mean field approximations for the GCA and the ECOHYDRY models it was necessary to have analytic expressions for the expectations of the global and local Flowlength values. As these expressions were not available, we carried out an instrumental work to derive them (Rodríguez et al., in review). In this work, we provided explicit theoretical expressions for the expected value and variance of the Flowlength index under random cover distribution and for a simple aggregated-pattern model; moreover, we illustrated the use of this kind of null model to disentangle the independent roles played by plant cover and pattern in dryland functioning, and we assessed the potential of using the deviation from the null model as indicator of ecosystem functional status and transitions. These analytic expressions were used to obtain and analyze the mean field approximation of the ECOHYDRY model, i.e., the BCA model of Kefi et al. (2007b) including the effects of both global and local feedbacks.
Note: For full references to papers quoted in this article see
